python-data

Numerical Analysis with Numpy

Numpy is probably the most significant numerical computing library (module) available for Python.

It is coded in both Python and C (for speed), providing high level access to extremely efficient computational routines.

Basic object of Numpy: The Array

One of the most basic building blocks in the Numpy toolkit is the Numpy N-dimensional array (ndarray), which is used for arrays of between 0 and 32 dimensions (0 meaning a “scalar”).

For example,

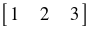matrix 1d is a 1d array, aka a vector, of shape (3,), and 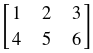matrix 2d is a 2d array of shape (2, 3).

While arrays are similar to standard Python lists (or nested lists) in some ways, arrays are much faster for lots of array operations.

However, arrays generally have to contain objects of the same type in order to benefit from this increased performance, and usually that means numbers.

In contrast, standard Python lists are very versatile in that each list item can be pretty much any Python object (and different to the other elements), but this versatility comes at the cost of drastically reduced speed.

Creating Arrays

ndarrays can be created in a number of ways.

From Python objects

Numpy includes a function called array which can be used to create arrays from numbers, lists of numbers or tuples of numbers.

E.g.

numpy.array([1,2,3])
numpy.array(7)

creates the 1d array [1,2,3], and number (scalar) 7 (albeit as an ndarray!).

Nested lists/tuples produce higher-dimensional arrays:

numpy.array([[1,2], [3,4]])

creates the 2d array

[[1 2]
 [3 4]]

NB: you can create arrays from dicts, lists of strings, and other data types, but the resulting ndarray will contain those objects as elements (instead of numbers), and might not behave as you expect!

Predefined arrays

There are also array creation functions to create specific types of arrays:

numpy.zeros((2,2))  # creates  [[ 0 0]
                    #           [ 0 0]]

numpy.ones(3)       # creates [ 1 1 1 ]

numpy.empty(2)      # creates [  6.89901308e-310,   6.89901308e-310]

NB: empty creates arrays of the right size but doesn’t set the values which start off with values determined by the previous memory content!

Random numbers

numpy.random contains a range of random-number generation functions.

Commonly used examples are

numpy.random.rand(d0, d1, ..., dn) # Uniform random values in a given shape, in range 0 to 1
numpy.random.randn(d0, d1,...,dn) # Standard normally distributed numbers (ie mean 0 and standard deviation 1)

Loading data from files

One to two dimensional arrays saved in comma-separated text format can be loaded using numpy.loadtxt:

arr2d = numpy.loadtxt('filename.csv', delimiter=",")    # The default delimiter is a space!

Similarly an array can be saved to the same format:

numpy.savetxt('filename.csv', arr2d_2, delimiter=",")    # The default delimiter is a space!)

Numpy also has an internal file format that can save and load N-dimensional arrays,

arrNd = numpy.load('inputfile.npy')

and

numpy.save('outputfile.npy', arrNd2)

NOTE: As usual, full paths are safer than relative paths, which are used here for brevity.

However, these files are generally not usable with other non-python programs.

Exercise : Create and save an array

Create a new script (“exercise_numpy_generate.py”) where you create and save a normally distributed random 1d array with 1000 values.

The array should have an offset (~mean value) of 42 and a standard deviation of 5.

Save the array to a csv file, (remember to set the delimiter to “,”) in your scripts folder, called “random_data.csv”.

Add a final line to the script that uses the os module’s listdir function to print csv files contained in the scripts folder.

Exercise
Answer

Working with ndarrays

Once an array has been loaded or created, it can be manipulated using either array object member functions, or numpy module functions.

Member functions

ndarrays are objects as covered briefly in the last section, and have useful attributes (~ data associated with the array):

ndarray.flags   Information about the memory layout of the array.
ndarray.shape   Tuple of array dimensions.
ndarray.strides Tuple of bytes to step in each dimension when traversing an array.
ndarray.ndim    Number of array dimensions.
ndarray.data    Python buffer object pointing to the start of the array’s data.
ndarray.size    Number of elements in the array.
ndarray.itemsize    Length of one array element in bytes.
ndarray.nbytes  Total bytes consumed by the elements of the array.
ndarray.base    Base object if memory is from some other object.

ndarray.dtype   Data-type of the array’s elements.


ndarray.T   Same as self.transpose(), except that self is returned if self.ndim < 2.
ndarray.real    The real part of the array.
ndarray.imag    The imaginary part of the array.
ndarray.flat    A 1-D iterator over the array.
ndarray.ctypes  An object to simplify the interaction of the array with the ctypes module.

as well as many useful member-functions including:

ndarray.reshape : Returns an array containing the same data with a new shape.
ndarray.resize  : Change shape and size of array in-place.
ndarray.transpose (or ndarray.T) : Returns a view of the array with axes transposed.
ndarray.swapaxes : Return a view of the array with axis1 and axis2 interchanged.
ndarray.flatten  : Return a copy of the array collapsed into one dimension.
ndarray.squeeze  : Remove single-dimensional entries from the shape of a.

ndarray.sort    : Sort an array, in-place.
ndarray.argsort : Returns the indices that would sort this array.
ndarray.diagonal: Return specified diagonals.
ndarray.nonzero :  Return the indices of the elements that are non-zero.

ndarray.argmax  : Return indices of the maximum values along the given axis.
ndarray.min : Return the minimum along a given axis.
ndarray.argmin  : Return indices of the minimum values along the given axis of a.
ndarray.ptp : Peak to peak (maximum - minimum) value along a given axis.
ndarray.clip    : Return an array whose values are limited to [min, max].
ndarray.conj : Complex-conjugate all elements.
ndarray.round : Return array with each element rounded to the given number of decimals.
ndarray.trace  : Return the sum along diagonals of the array.
ndarray.sum    : Return the sum of the array elements over the given axis.
ndarray.cumsum  : Return the cumulative sum of the elements along the given axis.
ndarray.mean    : Returns the average of the array elements along given axis.
ndarray.var : Returns the variance of the array elements, along given axis.
ndarray.std : Returns the standard deviation of the array elements along given axis.
ndarray.prod    : Return the product of the array elements over the given axis 
ndarray.cumprod : Return the cumulative product of the elements along the given axis.
ndarray.all : Returns True if all elements evaluate to True.
ndarray.any : Returns True if any of the elements of a evaluate to True.

including arithmetic operations on array elements:

+   Add 
-   Subtract 
*   Multiply 
/   Divide 
//  Divide arrays ("floor" division)
%   Modulus operator 
**  Exponent operator (`pow()`)  

# Logic
&   Logical AND
^   Logical XOR
|   Logical OR 
~   Logical Not

# Unary 
-   Negative 
+   Positive 
abs Absolute value
~   Invert

and comparison operators

==  Equals
<   Less than 
>   More than 
<=  Less than or equal
>=  More than or equal
!=  Not equal

Non-member functions

Additional functions operating on arrays exist, that the Numpy developers felt shouldn’t be included as member-functions. These include

# Trigonometric and hyperbolic functions
numpy.sin       : Sine 
numpy.cos       : Cosine
numpy.tan       : Tangent 
# And more trigonometric functions like `arcsin`, `sinh`

# Statistics 
numpy.median    : Calculate the median of an array
numpy.percentile : Return the qth percentile
numpy.cov       : Calculate the covariance matrix
numpy.histogram : Compute the histogram of data (does binning, not plotting!) 

# Differences
numpy.diff      : Element--element difference 
numpy.gradient  : Second-order central difference

# Manipulation 
numpy.concatenate : Join arrays along a given dimension 
numpy.rollaxis  : Roll specified axis backwards until it lies at given position
numpy.hstack    : Horizontally stack arrays
numpy.vstack    : Vertically stack arrays
numpy.repeat    : Repeat elements in an array
numpy.unique    : Find unique elements in an array

# Other
numpy.convolve  : Discrete linear convolution of two one-dimensional sequences
numpy.sqrt      : Square-root of each element
numpy.interp    : 1d linear interpolation

Exercise : Trying some Numpy functions

Let’s practice some of these Numpy functions.

Create a new script (“exercise_numpy_functions.py”), and create a 1d array with the values -100, -95, -90, … , 400 (i.e. start -100, stop 400, step 5). Call the variable that holds this array taxis as it corresponds to a time axis.

Now, generate a second, signal array (e.g. sig) from the first, consisting of two parts:

  • a normally distributed noise (zero mean, standard deviation 2) baseline up to the point where taxis is equal to 0.
  • Increasing exponential “decay”, i.e. C ( 1 - e^{-kt} ) with the same with the same noise as the negative time component, with C = 10 and k = 1/50.

Lastly combine the two 1d arrays into an 2d array, where each 1d array forms a column of the 2d array (in the order taxis, then sig).

Save the array to a csv file, (remember to set the delimeter to “,”) in your scripts folder, called “growth_data.csv”.

List the script folder csv files as before to confirm that the file has been created and is in the correct location.

Excerise
Answer

Accessing elements

Array elements can be accessed using the same slicing mechanism as lists; e.g. if we have a 1d array assigned to arr1 containing [5, 4, 3, 2, 1], then

  • arr1[4] accesses the 5th element = 1
  • arr1[2:] accesses the 3rd element onwards = [3,2,1]
  • arr1[-1] accesses the last element = 1
  • arr1[-1::-1] accesses the last element onwards with step -1, = [1,2,3,4,5] (i.e. the elements reversed!)

Similarly higher dimensional arrays are accessed using comma-separated slices.
If we have a 2d array;

a = numpy.array([[ 11, 22],
                 [ 33, 44]])

(which we also represent on one line as [[ 11, 22], [ 33, 44]]), then

  • a[0] accesses the first row = [11, 22]
  • a[0,0] accesses the first element of the first row = 11
  • a[-1,-1] accesses the last element of the last row = 44
  • a[:,0] accesses all elements of the first column = [11,33]
  • a[-1::-1] reverses the row order = [[33, 44], [11,22]]
  • a[-1::-1,-1::-1] reverses both row and column order = [[ 44, 33], [ 22, 11]]

The same logic is extended to higher-dimensional arrays.

Using binary arrays (~masks)

In addition to the slice notation, a very useful feature of Numpy is logical indexing, i.e. using a binary array which has the same shape as the array in question to access those elements for which the binary array is True.

Note that the returned elements are always returned as a flattened array. E.g.

arr1 = np.array([[ 33, 55], 
                 [ 77, 99]])
mask2 = np.array([[True, False], 
                 [False, True]])
print( arr1[ mask2 ])

would result in

[33, 99]

being printed to the terminal.

The usefulness of this approach should become apparent in a later exercise!

Exercise : Load and analyze data

Write a new script to

  • Load the numpy data you saved in the previous exercise (“growth_data.csv”)
  • Print to the console the following statistics for the signal column
    • mean
    • median
    • standard deviation
    • shape
    • histogrammed information (10 bins)
  • Next, select only the signal point for taxis >= 0 and print the same statistics
Excerise
Answer

Dealing with NaN and infinite values

Generally speaking, Python handles division by zero as an error; to avoid this you would usually need to check whether a denominator is non-zero or not using an if-block to handle the cases separately.

Numpy on the other hand, handles such events in a more sensible manner.

Not a Number

NaNs (numpy.nan) (abbreviation of “Not a Number”) occur when a computation can’t return a sensible number; for example a Numpy array element 0 when divided by 0 will give nan.

They can also be used can be used to represent missing data.

NaNs can be handled in two ways in Numpy;

  • Find and select only non-NaNs, using numpy.isnan to identify NaNs
  • Use a special Nan-version of the Numpy function you want to perform (if it exists!)

For example, if we want to perform a mean or maximum operation, Numpy offers nanmean and nanmax respectively. Additional NaN-handling version of argmax, max, min, sum, argmin, mean, std, and var exist (all by prepending nan to the function name).

When a pre-defined NaN-version of the function you need doesn’t exist, you will need to select only non-NaN values; e.g.

allnumbers = np.array([np.nan, 1, 2, np.nan, np.nan])

# We can get the mean already
print(np.nanmean(allnumbers))                                 # Prints 1.5 to the terminal 

# But a nan version of median doesn't exist, and if we try 
print(np.median( allnumbers ))                              # Prints nan to the terminal 
# The solution is to use
validnumbers = allnumbers[ ~ np.isnan(allnumbers) ]
print(np.median( validnumbers ))                            # Prints 1.5 to the terminal

To Infinity, and beyond…

Similarly, a Numpy array non-zero element divided by 0 gives inf, Numpy’s representation of infinity.

However, Numpy does not have any functions that handle infinity in the same way as the nan-functions (i.e. by essentially ignoring them). Instead, e.g. the mean of an array containing infinity, is infinity (as it should be!). If you want to remove infinities from calculations, then this is done in an analogous way to the NaNs;

allnumbers = np.array([np.inf, 5, 6, np.inf])
print(allnumbers.mean())                                # prints inf to the terminal
finite_numbers = allnumbers[ ~np.isinf(allnumbers) ] 
print(finite_numbers.mean())                            # prints 5.5 to the terminal

Tip: np.isfinite for both

np.isfinite will return an array that contains True everywhere the
input array is neither infinite nor a NaN.

Next steps: Visualization helps!

Now that we have a basic understanding of how to create and manipulate arrays, it’s already starting to become clear that producing numbers alone makes understanding the data difficult.

With that in mind then, let’s start working on visualization, and perform further Numpy analyses there!